The Big Con of SPR - and How to Solve it
Understanding the environmental noise problem encountered and the high measurement precision needed in with surface plasmon resonance (and all refractometric biosensors) requires fundamental knowledge not only of how the desired binding signal is acquired in this technique, but also why we detect changes (noise) we are not interested in measuring.
Signal Processing- The Basics
Let’s begin by thinking of what we want to achieve with a biosensing technology such as SPR. Like most biosensors, the aim is to detect specific molecular interactions in real-time. But the bigger question we must ask first is: how can we measure only this specific molecular interaction and nothing else? In other words, how can we measure the signal without measuring the environmental noise buried in real space?
To develop such a sensing concept, we need a basic understanding of signal processing. This is not an easy task, mostly because the concept used in signal processing quickly become abstract. To avoid confusion, we use an analogy for an array of molecular interactions we aim to detect: a simple image, such as the one you could get with your smartphone camera. In the language of signal processing, a smartphone image and an array of molecular interactions is the same. So, what is an image, mathematically? It is just a combination of numbers, arranged in what we call a matrix (a table, of sorts). The numbers inside this matrix specify the intensity of light in the image at specific coordinates.
In many cases, the biggest challenge when taking a photograph is to image exactly what is in front of the camera, e.g. the faces of the people in the picture; in this respect, it is very similar to detecting biosignals. The issue that both these processes face is also the same: noise. Noise is essentially a range of signals that we don’t want to acquire, because they interfere with the proper readout of the signal (in our analogy, the faces of the pictured people) we do want. It can originate from environmental influences: for instance, if you took a picture facing the sun, the faces of the people you want to picture would not appear, because the sunlight overexposes your sensor. This issue stems from problems with data acquisition, e.g. the settings you use on your camera when taking a picture. One way to fix this is to directly account for environmental noise during the acquisition of the data; however, this is more challenging than it sounds, because you don’t always know where the noise will come from and how much it will interfere with the signal of interest. Usually, it only becomes evident once the data (in our example, still the image) is already acquired. However, this remains problematic, because not all environmental noise can be filtered out once the signal is obtained. Indeed, an overexposed photograph can be filtered to enhance certain contrasts, but filters cannot entirely remove the overexposed nature of the image. This is because every pixel in the image is immersed in environmental noise and these signals fully overlap: they can no longer be fully discriminated. For this reason, it is crucial to exclude as much noise as possible before data acquisition. Filtering noise is the key to this; but how can it be achieved before signal acquisition? How is it different than using filters on a smartphone?
Filtering Signals
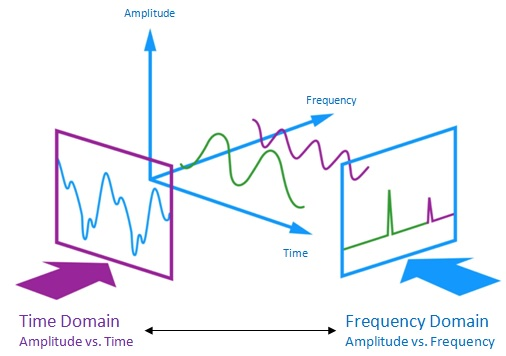
Filtering can be done in different ways, and more importantly, it can be done in different spaces: in real space, or in Fourier space. Real space describes space the way we are most familiar with it, the way we see it, in the typical three dimensions. Fourier space on the other hand isn’t a “space” the way we conceive it in our minds, but a mathematical analogy of this. It is used to convert images from the real space in terms of their frequency components. The tool that we use to perform this transformation is called the Fourier transform. What this looks like mathematically is a conversion of a complicated function (representing the raw signal or the raw image) into several simpler functions. Figure 1 depicts this concept; as you can see in this figure, the raw signal shown in the time domain (in real space) can be separated into simpler components in the so-called frequency. When graphically representing these components in the frequency domain, we obtain a very different graph. The essential take-away is the following: although the frequency domain graph looks very different, it is representing the same original signal in real space, just in a different manner.
Images in Fourier Space
Signals can be represented both in real space and in Fourier space; this applies to images as well! Below is an example of an image in real space (on the left) vs. image in Fourier space (on the right). In Fourier space, signals closest to the center are low-frequency signals, while high-frequency signals are found in the periphery.

Although these images look vastly different, they represent the same information in different manners. In short: there is more than one way to see an image (and biosignals)!Why is this important and why is it useful to represent biosignals and images in Fourier space instead of real space? It all comes back to the original question we asked at the very beginning of this article: When trying to detect a specific signal, e.g. a molecular interaction, or trying to capture a specific image, how can we detect exactly what we would like to detect, and nothing else? The answer to this is to perform the measurement in Fourier space instead of real space.
But why? Although analyzing signals and images in real space is much more intuitive, it is much harder to handle the data in this space once it is acquired. As mentioned previously, data acquisition is often faulty, because we can not always optimize how we acquire our data in a way that excludes any unwanted signal. This is particularly difficult with biosignals, because we can not see environmental noise the way we do an image. This is why we must use filters before the data is acquired, unlike applying a filter to a taken image on our smartphones. However, when looking at the signal acquired in the time domain in figure 1 for example, you will notice that filtering out unwanted signal becomes a tedious task. Just by looking at this function, how can we know what parts of it we want, and what parts we don’t want? Moreover, how can we remove those parts across the entire function? Likewise, for the image, how can we filter out the noise and keep the desired information? The truth is, unless we go through the process of trial and error, it is very difficult to do this in real space. However, when looking at the same information in Fourier space, things become much simpler. Looking at figure 2 for instance, in the right image, we see a bright spot in the middle that dims as we get closer to the edge; this means that there is a lot of low-frequency signals (slow or long-ranged) and only few high-frequency signals (fast or short-ranged) in the image. It so happens that noisy signal belongs to low-frequency ranges: knowing this, we can simply filter out the signal in the center of the image, an keep everything else around it. Similarly, with the signal in figure 1, we can remove the signal comprised within the peak appearing at low frequency, and keep the peak at high frequency. Once the filtering is done, we use the inverse Fourier transform to convert the newly filtered data from the Fourier space back into real space, thus obtaining a “clean” signal that we can interpret!
Signals in Surface Plasmon Resonance
At this stage, it may be unclear how this relates to the surface plasmon resonance technology. The aim of SPR is to detect biosignals. Because the signals we want to detect with SPR are mingled with a majority of noise component (environmental noise) we are not interested in, we are faced with the problem described throughout this article: how to detect signal without noise. This is crucial for SPR in particular, as without a robust process to solve this issue, the signal we want to detect gets very easily lost in a sea of noise. In practice, this is what makes SPR so challenging; it is extremely sensitive, but this sensitivity does not discriminate between desired signal and the noise. Indeed, SPR samples its data in real space. Every data point we sample contains noise and the weak signal is diluted over all. In order to get enough of the interesting signal, we need to sample many data points. This means that we acquire monumental amounts of noise.
Still confused? An analogy to put this into perspective.
Imagine you are standing on a standard scale, one you would use to weigh yourself, with a shot glass containing a bit of water. In this analogy, you represent the environmental noise, and the water you pour into the glass represents the signal, i.e. the change you want to detect. If a few drops of water were added to the shot glass, the change in weight would most likely not be detected by the scale you are standing on, as the increment is too small. To detect this change on that scale, it would need to have an extremely high precision (i.e. be able to measure in the gram range) whilst also maintaining a large range of weights (e.g. 0-100kg). If you were to weigh the shot glass alone on a new scale measuring only in the gram-range (e.g. 0-10g) instead of the kilogram range however, the added weight of the water would be detected. Thus, the new scale can detect the changes with higher accuracy. More importantly, the absolute precision required to detect the added water, in this example, 1g, remains the same for both scales; however, when looking at the relative precision of both scales, the smaller scale would show a significant advantage. Indeed, 1g in a measuring range of 10g is much less precise than 1g in a range of 100kg… Surface plasmon resonance is analog to the big scale: it requires extremely high precision to detect signals of interest, whilst also having to sample a very large range of signals.

In a Nutshell
How can we untangle these signals from each other across all the data points we sample? Could it be possible to avoid this problem and circumvent the noise acquisition completely? By sampling our data in Fourier space instead of real space, we achieve just that. Signal and noise are nicely separated; if we place out detector at the signal location we can acquire only the signal, while we do not even see the noise. This brings a significant advantage to the table: our detector no longer requires extreme relative precision. The same way we do not need a 100kg-ranged scale with 1g precision to measure a few drops of water added to a glass, we do not need a signal detector sampling a large range with a high precision. We can simply use a cheaper scale or signal detector with a much smaller range and much smaller relative precision. SPR measures signals the hard way; how can we design a biosensor that does this the smart way? Has such a biosensor ever been made? Find out in the next article!
References
http://play.fallows.ca/wp/radio/ham-radio/signal-analysis-morse-decoder/
biorender.com
Frutiger, Andreas, Christof Fattinger, and János Vörös. “Ultra-Stable Molecular Sensors by Sub-Micron Referencing and Why They Should Be Interrogated by Optical Diffraction—Part I. The Concept of a Spatial Affinity Lock-in Amplifier.” Sensors 21.2 (2021): 469.
Frutiger, Andreas, et al. “Ultra Stable Molecular Sensors by Submicron Referencing and Why They Should Be Interrogated by Optical Diffraction—Part II. Experimental Demonstration.” Sensors 21.1 (2021): 9.

